Functional Swift
Learn core concepts of functional programming with Swift and leverage them in real world code.
by Chris Eidhof, Florian Kugler, and Wouter Swierstra
Introduction
Why write this book? There’s plenty of documentation on Swift readily available from Apple, and there are many more books on the way. Why does the world need yet another book on yet another programming language?
This book tries to teach you to think functionally. We believe that Swift has the right language features to teach you how to write functional programs. But what makes a program functional? And why bother learning about this in the first place?
It’s hard to give a precise definition of functional programming — in the same way, it’s hard to give a precise definition of object-oriented programming, or any other programming paradigm for that matter. Instead, we’ll try to focus on some of the qualities that we believe well-designed functional programs in Swift should exhibit:
Modularity: Rather than thinking of a program as a sequence of assignments and method calls, functional programmers emphasize that each program can be repeatedly broken into smaller and smaller pieces, and all these pieces can be assembled using function application to define a complete program. Of course, this decomposition of a large program into smaller pieces only works if we can avoid sharing state between the individual components. This brings us to our next point.
A Careful Treatment of Mutable State: Functional programming is sometimes (half-jokingly) referred to as ‘value-oriented programming.’ Object-oriented programming focuses on the design of classes and objects, each with their own encapsulated state. Functional programming, on the other hand, emphasizes the importance of programming with values, free of mutable state or other side effects. By avoiding mutable state, functional programs can be more easily combined than their imperative or object-oriented counterparts.
Types: Finally, a well-designed functional program makes careful use of types. More than anything else, a careful choice of the types of your data and functions will help structure your code. Swift has a powerful type system that, when used effectively, can make your code both safer and more robust.
We feel these are the key insights that Swift programmers may learn from the functional programming community. Throughout this book, we’ll illustrate each of these points with many examples and case studies.
In our experience, learning to think functionally isn’t easy. It challenges the way we’ve been trained to decompose problems. For programmers who are used to writing for loops, recursion can be confusing; the lack of assignment statements and global state is crippling; and closures, generics, higher-order functions, and monads are just plain weird.
Throughout this book, we’ll assume that you have previous programming experience in Objective-C (or some other object-oriented language). We won’t cover Swift basics or teach you to set up your first Xcode project, but we will try to refer to existing Apple documentation when appropriate. You should be comfortable reading Swift programs and familiar with common programming concepts, such as classes, methods, and variables. If you’ve only just started to learn to program, this may not be the right book for you.
In this book, we want to demystify functional programming and dispel some of the prejudices people may have against it. You don’t need to have a PhD in mathematics to use these ideas to improve your code! Functional programming isn’t the only way to program in Swift. Instead, we believe that learning about functional programming adds an important new tool to your toolbox, which will make you a better developer in any language.
Updates to the Book
As Swift evolves, we’ll continue to make updates and enhancements to this book. Should you encounter any mistakes, or if you’d like to send any other kind of feedback our way, please file an issue in our GitHub repository.
Acknowledgements
We’d like to thank the numerous people who helped shape this book. We wanted to explicitly mention some of them:
Natalye Childress is our copy editor. She has provided invaluable feedback, not only making sure the language is correct and consistent, but also making sure things are understandable.
Sarah Lincoln designed the cover and the layout of the book.
Wouter would like to thank Utrecht University for letting him take time to work on this book.
We’d also like to thank the beta readers for their feedback during the writing of this book (listed in alphabetical order):
Adrian Kosmaczewski, Alexander Altman, Andrew Halls, Bang Jun-young, Daniel Eggert, Daniel Steinberg, David Hart, David Owens II, Eugene Dorfman, f-dz-v, Henry Stamerjohann, J Bucaran, Jamie Forrest, Jaromir Siska, Jason Larsen, Jesse Armand, John Gallagher, Kaan Dedeoglu, Kare Morstol, Kiel Gillard, Kristopher Johnson, Matteo Piombo, Nicholas Outram, Ole Begemann, Rob Napier, Ronald Mannak, Sam Isaacson, Ssu Jen Lu, Stephen Horne, TJ, Terry Lewis, Tim Brooks, Vadim Shpakovski.
Chris, Florian, and Wouter
Thinking Functionally
Functions in Swift are first-class values, i.e. functions may be passed as arguments to other functions, and functions may return new functions. This idea may seem strange if you’re used to working with simple types, such as integers, booleans, or structs. In this chapter, we’ll try to explain why first-class functions are useful and provide our first example of functional programming in action.
Throughout this chapter, we’ll use both functions and methods. Methods are a special case of functions: they are functions defined on a type.
Example: Battleship
We’ll introduce first-class functions using a small example: a non-trivial function that you might need to implement if you were writing a Battleship-like game. The problem we’ll look at boils down to determining whether or not a given point is in range, without being too close to friendly ships or to us.
As a first approximation, you might write a very simple function that checks whether or not a point is in range. For the sake of simplicity, we’ll assume that our ship is located at the origin. We can visualize the region we want to describe in Figure 1:
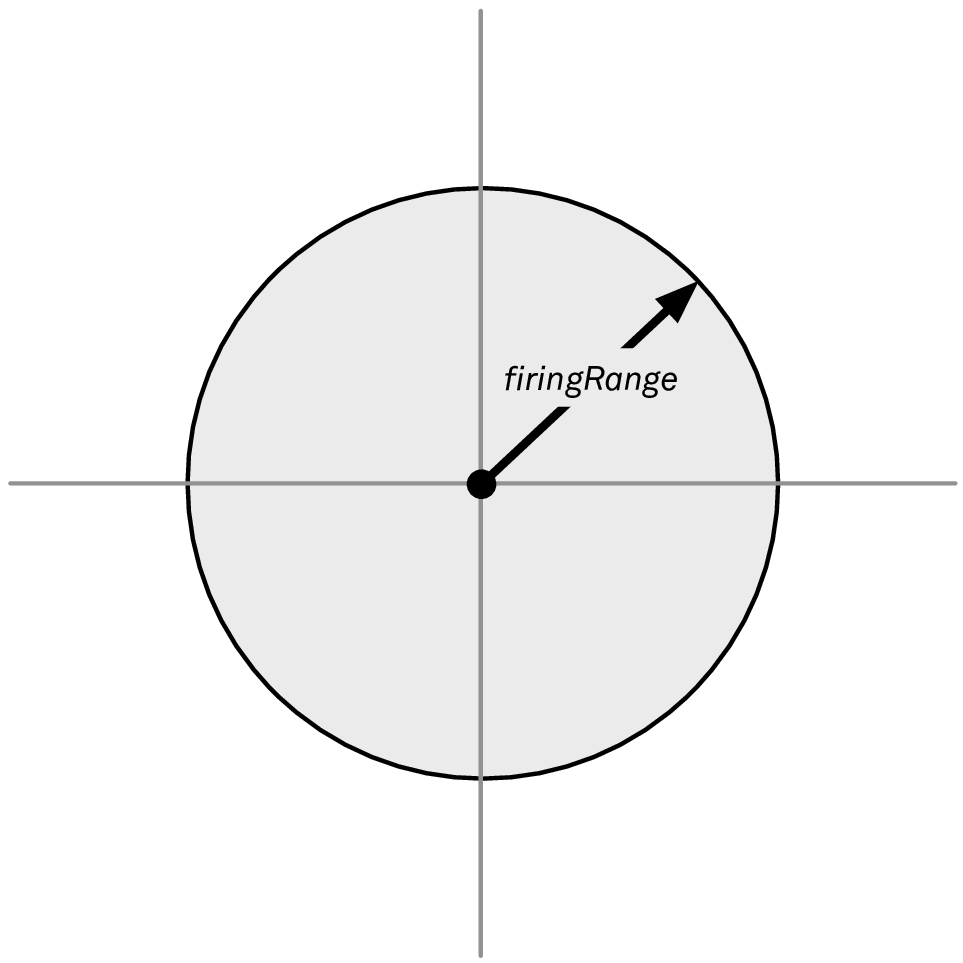
Figure 1: The points in range of a ship located at the origin
First, we’ll define two types, Distance and Position:
typealias Distance = Double
struct Position {
var x: Double
var y: Double
}
Note that we’re using Swift’s typealias construct, which allows us to introduce a new name for an existing type. We define Distance to be an alias of Double. This will make our API more expressive.
Now we add a method to Position, within(range:), which checks that a point is in the grey area in Figure 1. Using some basic geometry, we can write this method as follows:
extension Position {
func within(range: Distance) -> Bool {
return sqrt(x * x + y * y) <= range
}
}
This works fine, if you assume that we’re always located at the origin. But suppose the ship may be at a location other than the origin. We can update our visualization in Figure 2:
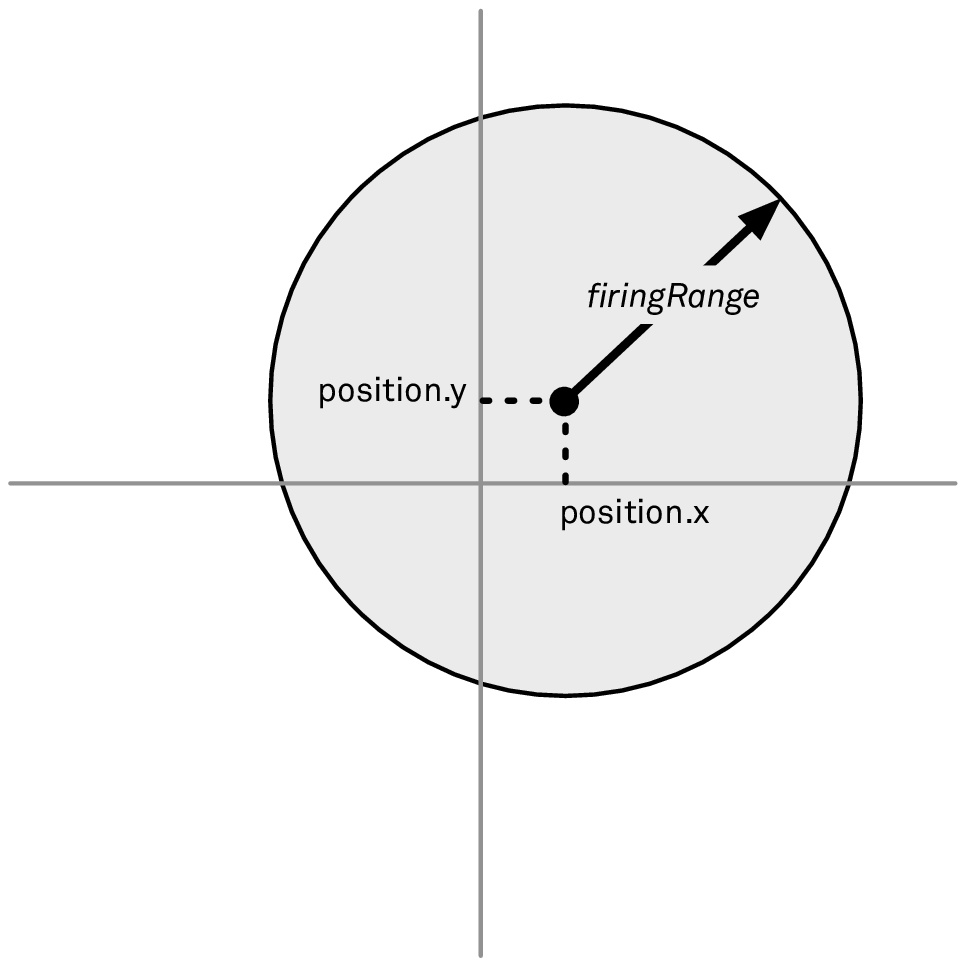
Figure 2: Allowing the ship to have its own position
To account for this, we introduce a Ship struct that has a position property:
struct Ship {
var position: Position
var firingRange: Distance
var unsafeRange: Distance
}
For now, just ignore the additional property, unsafeRange. We’ll come back to this in a bit.
We extend the Ship struct with a method, canEngage(ship:), which allows us to test if another ship is in range, irrespective of whether we’re located at the origin or at any other position:
extension Ship {
func canEngage(ship target: Ship) -> Bool {
let dx = target.position.x - position.x
let dy = target.position.y - position.y
let targetDistance = sqrt(dx * dx + dy * dy)
return targetDistance <= firingRange
}
}
But now you realize that you also want to avoid targeting ships if they’re too close to you. We can update our visualization to illustrate the new situation in Figure 3, where we want to target only those enemies that are at least unsafeRange away from our current position:
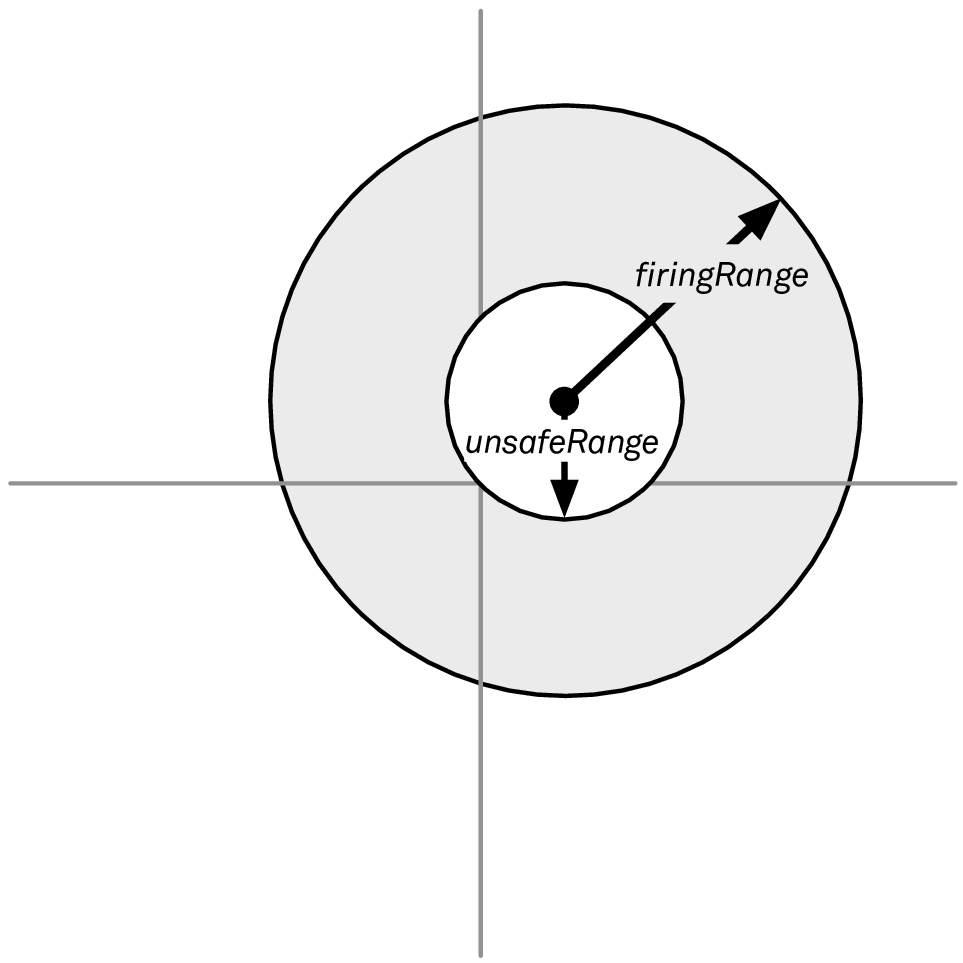
Figure 3: Avoiding engaging enemies too close to the ship
As a result, we need to modify our code again, making use of the unsafeRange property:
extension Ship {
func canSafelyEngage(ship target: Ship) -> Bool {
let dx = target.position.x - position.x
let dy = target.position.y - position.y
let targetDistance = sqrt(dx * dx + dy * dy)
return targetDistance <= firingRange && targetDistance > unsafeRange
}
}
Finally, you also need to avoid targeting ships that are too close to one of your other ships. Once again, we can visualize this in Figure 4:
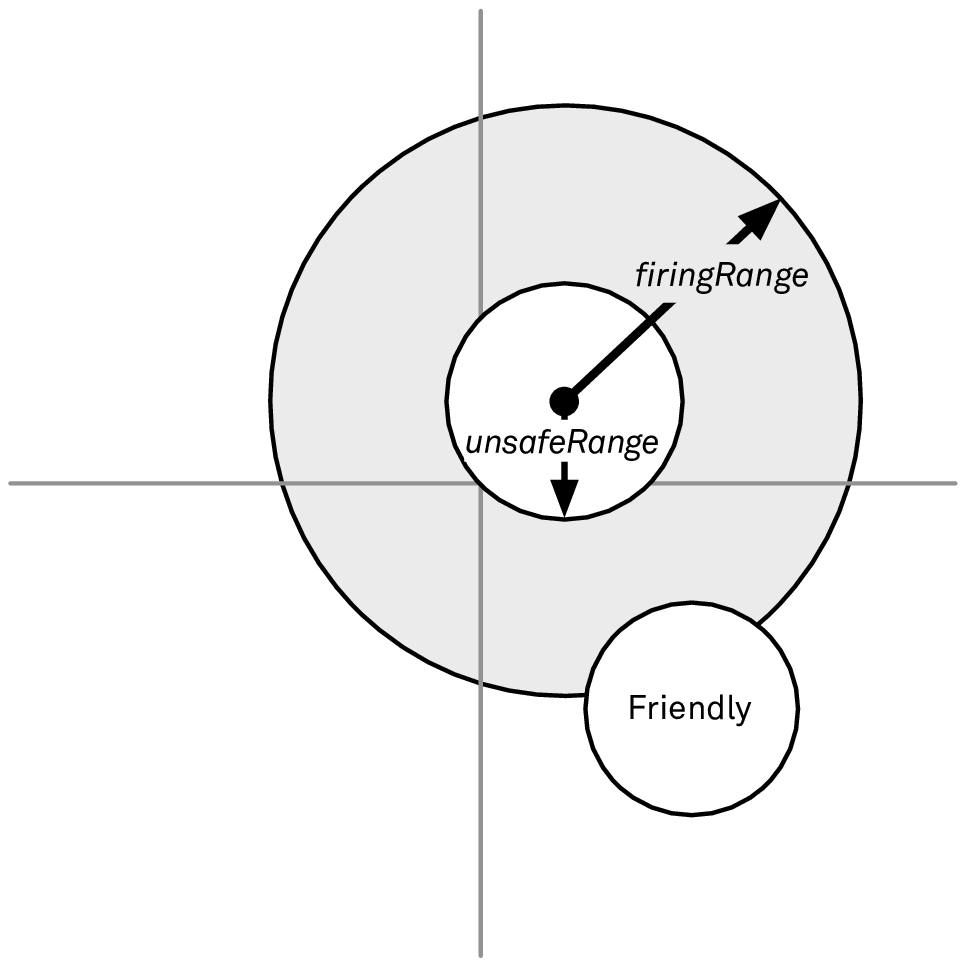
Figure 4: Avoiding engaging targets too close to friendly ships
Correspondingly, we can add a further argument that represents the location of a friendly ship to our canSafelyEngage(ship:) method:
extension Ship {
func canSafelyEngage(ship target: Ship, friendly: Ship) -> Bool {
let dx = target.position.x - position.x
let dy = target.position.y - position.y
let targetDistance = sqrt(dx * dx + dy * dy)
let friendlyDx = friendly.position.x - target.position.x
let friendlyDy = friendly.position.y - target.position.y
let friendlyDistance = sqrt(friendlyDx * friendlyDx +
friendlyDy * friendlyDy)
return targetDistance <= firingRange
&& targetDistance > unsafeRange
&& (friendlyDistance > unsafeRange)
}
}
As this code evolves, it becomes harder and harder to maintain. This method expresses a complicated calculation in one big lump of code, but we can clean this code up a bit by adding a helper method and a computed property on Position for the geometric calculations:
extension Position {
func minus(_ p: Position) -> Position {
return Position(x: x - p.x, y: y - p.y)
}
var length: Double {
return sqrt(x * x + y * y)
}
}
Using those helpers, the method becomes the following:
extension Ship {
func canSafelyEngageShip2(target: Ship, friendly: Ship) -> Bool {
let targetDistance = target.position.minus(position).length
let friendlyDistance = friendly.position.minus(target.position).length
return targetDistance <= firingRange
&& targetDistance > unsafeRange
&& (friendlyDistance > unsafeRange)
}
}
This is already much more readable, but we want to go one step further and take a more declarative route to specifying the problem at hand.
First-Class Functions
In the current incarnation of the canSafelyEngage(ship:friendly) method, its behavior is encoded in the combination of boolean conditions the return value is comprised of. While it’s not too hard to figure out what this method does in this simple case, we want to have a solution that’s more modular.
We already introduced helper methods on Position to clean up the code for the geometric calculations. In a similar fashion, we’ll now add functions to test whether a region contains a point in a more declarative manner.
The original problem boiled down to defining a function that determined when a point was in range or not. The type of such a function would be something like this:
func pointInRange(point: Position) -> Bool {
// Implement method here
}The type of this function is going to be so important that we’re going to give it a separate name:
typealias Region = (Position) -> Bool
From now on, the Region type will refer to functions transforming a Position to a Bool. This isn’t strictly necessary, but it can make some of the type signatures that we’ll see below a bit easier to digest.
Instead of defining an object or struct to represent regions, we represent a region by a function that determines if a given point is in the region or not. If you’re not used to functional programming, this may seem strange, but remember: functions in Swift are first-class values! We consciously chose the name Region for this type, rather than something like CheckInRegion or RegionBlock. These names suggest that they denote a function type, yet the key philosophy underlying functional programming is that functions are values, no different from structs, integers, or booleans — using a separate naming convention for functions would violate this philosophy.
We’ll now write several functions that create, manipulate, and combine regions.
The first region we define is a circle, centered around the origin:
func circle(radius: Distance) -> Region {
return { point in point.length <= radius }
}
Note that, given a radius r, the call circle(radius: r) returns a function. Here we use Swift’s notation for closures to construct the function we wish to return. Given an argument position, point, we check that the point is in the region delimited by a circle of the given radius centered around the origin.
Of course, not all circles are centered around the origin. We could add more arguments to the circle function to account for this. To compute a circle that’s centered around a certain position, we just add another argument representing the circle’s center and make sure to account for this value when computing the new region:
func circle2(radius: Distance, center: Position) -> Region {
return { point in point.minus(center).length <= radius }
}
However, if we we want to make the same change to more primitives (for example, imagine we not only had circles, but also rectangles or other shapes), we might need to duplicate this code. A more functional approach is to write a region transformer instead. This function shifts a region by a certain offset:
func shift(_ region: @escaping Region, by offset: Position) -> Region {
return { point in region(point.minus(offset)) }
}
Whenever a function parameter (for example,
region) is used after the function returns, it needs to be marked as@escaping. The compiler tells us when we forget to add this. For more information, see the section on “Escaping Closures” in Apple’s book, The Swift Programming Language.
The call shift(region, by: offset) moves the region to the right and up by offset.x and offset.y, respectively. We need to return a Region, which is a function from a point to a boolean value. To do this, we start writing another closure, introducing the point we need to check. From this point, we compute a new point by subtracting the offset. Finally, we check that this new point is in the original region by passing it as an argument to the region function.
This is one of the core concepts of functional programming: rather than creating increasingly complicated functions such as circle2, we’ve written a function, shift(_:by:), that modifies another function. For example, a circle that’s centered at (5, 5) and has a radius of 10 can now be expressed like this:
let shifted = shift(circle(radius: 10), by: Position(x: 5, y: 5))
There are lots of other ways to transform existing regions. For instance, we may want to define a new region by inverting a region. The resulting region consists of all the points outside the original region:
func invert(_ region: @escaping Region) -> Region {
return { point in !region(point) }
}
We can also write functions that combine existing regions into larger, complex regions. For instance, these two functions take the points that are in both argument regions or either argument region, respectively:
func intersect(_ region: @escaping Region, with other: @escaping Region)
-> Region {
return { point in region(point) && other(point) }
}
func union(_ region: @escaping Region, with other: @escaping Region)
-> Region {
return { point in region(point) || other(point) }
}
Of course, we can use these functions to define even richer regions. The difference function takes two regions as argument — the original region and the region to be subtracted — and constructs a new region function for all points that are in the first, but not in the second, region:
func subtract(_ region: @escaping Region, from original: @escaping Region)
-> Region {
return intersect(original, with: invert(region))
}
This example shows how Swift lets you compute and pass around functions no differently than you would integers or booleans. This enables us to write small primitives (such as circle) and to build a series of functions on top of these primitives. Each of these functions modifies or combines regions into new regions. Instead of writing complex functions to solve a very specific problem, we can now use many small functions that can be assembled to solve a wide variety of problems.
Now let’s turn our attention back to our original example. With this small library in place, we can refactor the complicated canSafelyEngage(ship:friendly:) method as follows:
extension Ship {
func canSafelyEngageShip(target: Ship, friendly: Ship) -> Bool {
let rangeRegion = subtract(circle(radius: unsafeRange),
from: circle(radius: firingRange))
let firingRegion = shift(rangeRegion, by: position)
let friendlyRegion = shift(circle(radius: unsafeRange),
by: friendly.position)
let resultRegion = subtract(friendlyRegion, from: firingRegion)
return resultRegion(target.position)
}
}
This code defines two regions: firingRegion and friendlyRegion. The region that we’re interested in is computed by taking the difference between these regions. By applying this region to the target ship’s position, we can compute the desired boolean.
Compared to the original canSafelyEngage(ship:friendly:) method, the refactored method provides a more declarative solution to the same problem by using the Region functions. We argue that the latter version is easier to understand because the solution is compositional. You can study each of its constituent regions, such as firingRegion and friendlyRegion, and see how these are assembled to solve the original problem. The original, monolithic method, on the other hand, mixes the description of the constituent regions and the calculations needed to describe them. Separating these concerns by defining the helper functions we presented previously increases the compositionality and legibility of complex regions.
Having first-class functions is essential for this to work. Objective-C also supports first-class functions, or blocks. It can, unfortunately, be quite cumbersome to work with blocks. Part of this is a syntax issue: both the declaration of a block and the type of a block aren’t as straightforward as their Swift counterparts. In later chapters, we’ll also see how generics make first-class functions even more powerful, going beyond what is easy to achieve with blocks in Objective-C.
The way we’ve defined the Region type does have its disadvantages. Here we’ve chosen to define the Region type as a simple type alias for (Position) -> Bool functions. Instead, we could’ve chosen to define a struct containing a single function:
struct Region {
let lookup: Position -> Bool
}
Instead of the free functions operating on our original Region type, we could then define similar methods as extensions to this struct. And instead of assembling complex regions by passing them to functions, we could then repeatedly transform a region by calling these methods:
rangeRegion.shift(ownPosition).difference(friendlyRegion)
The latter approach has the advantage of requiring fewer parentheses. Furthermore, Xcode’s autocompletion can be invaluable when assembling complex regions in this fashion. For the sake of presentation, however, we’ve chosen to use a simple typealias to highlight how higher-order functions can be used in Swift.
Furthermore, it’s worth pointing out that we can’t inspect how a region was constructed: is it composed of smaller regions? Or is it simply a circle around the origin? The only thing we can do is to check whether a given point is within a region or not. If we want to visualize a region, we’d have to sample enough points to generate a (black and white) bitmap.
In a later chapter, we’ll sketch an alternative design that will allow you to answer these questions.
The naming we’ve used in this chapter, and throughout this book, goes slightly against the Swift API design guidelines. Swift’s guidelines are designed with method names in mind. For example, if
intersectwere defined as a method, it would need to be calledintersectingorintersected, because it returns a new value rather than mutating the existing region. However, we decided to use basic forms likeintersectwhen writing top-level functions.
Type-Driven Development
In the introduction, we mentioned how functional programs take the application of functions to arguments as the canonical way to assemble bigger programs. In this chapter, we’ve seen a concrete example of this functional design methodology. We’ve defined a series of functions for describing regions. Each of these functions isn’t very powerful on its own. Yet together, the functions can describe complex regions you wouldn’t want to write from scratch.
The solution is simple and elegant. It’s quite different from what you might write if you had naively refactored the canSafelyEngage(ship:friendly:) method into separate methods. The crucial design decision we made was how to define regions. Once we chose the Region type, all the other definitions followed naturally. The moral of the example is choose your types carefully. More than anything else, types guide the development process.
Notes
The code presented here is inspired by the Haskell solution to a problem posed by the United States Advanced Research Projects Agency (ARPA) by Hudak and Jones (1994).
Objective-C added support for first-class functions with the addition of blocks: you can use functions and closures as parameters and easily define them inline. However, working with them isn’t nearly as convenient in Objective-C as it is in Swift, even though they’re semantically equivalent.
Historically, the idea of first-class functions can be traced as far back as Church’s lambda calculus (Church 1941; Barendregt 1984). Since then, the concept has made its way into numerous (functional) programming languages, including Haskell, OCaml, Standard ML, Scala, and F#.
Case Study: Wrapping Core Image
The previous chapter introduced the concept of higher-order functions and showed how functions can be passed as arguments to other functions. However, the example used there may seem far removed from the ‘real’ code that you write on a daily basis. In this chapter, we’ll show how to use higher-order functions to write a small, functional wrapper around an existing, object-oriented API.
Core Image is a powerful image processing framework, but its API can be a bit clunky to use at times. The Core Image API is loosely typed — image filters are configured using key-value coding. It’s all too easy to make mistakes in the type or name of arguments, which can result in runtime errors. The new API we develop will be safe and modular, exploiting types to guarantee the absence of such runtime errors.
Don’t worry if you’re unfamiliar with Core Image or can’t understand all the details of the code fragments in this chapter. The goal isn’t to build a complete wrapper around Core Image, but instead to illustrate how concepts from functional programming, such as higher-order functions, can be applied in production code.
The Filter Type
One of the key classes in Core Image is the CIFilter class, which is used to create image filters. When you instantiate a CIFilter object, you (almost) always provide an input image via the kCIInputImageKey key, and then retrieve the filtered result via the outputImage property. Then you can use this result as input for the next filter.
In the API we’ll develop in this chapter, we’ll try to encapsulate the exact details of these key-value pairs and present a safe, strongly typed API to our users. We define our own Filter type as a function that takes an image as its parameter and returns a new image:
typealias Filter = (CIImage) -> CIImage
This is the base type we’re going to build upon.
Building Filters
Now that we have the Filter type defined, we can start defining functions that build specific filters. These are convenience functions that take the parameters needed for a specific filter and construct a value of type Filter. These functions will all have the following general shape:
func myFilter(...) -> Filter
Note that the return value, Filter, is a function as well. Later on, this will help us compose multiple filters to achieve the image effects we want.
Blur
Let’s define our first simple filters. The Gaussian blur filter only has the blur radius as its parameter:
func blur(radius: Double) -> Filter {
return { image in
let parameters: [String: Any] = [
kCIInputRadiusKey: radius,
kCIInputImageKey: image
]
guard let filter = CIFilter(name: "CIGaussianBlur",
withInputParameters: parameters)
else { fatalError() }
guard let outputImage = filter.outputImage
else { fatalError() }
return outputImage
}
}
That’s all there is to it. The blur function returns a function that takes an argument image of type CIImage and returns a new image (return filter.outputImage). Because of this, the return value of the blur function conforms to the Filter type we defined previously as (CIImage) -> CIImage.
Note how we use guard statements to unwrap the optional values returned from the CIFilter initializer, as well as from the filter’s outputImage property. If any of those values would be nil, it’d be a case of a programming error where we, for example, have supplied the wrong parameters to the filter. Using the guard statement in conjunction with a fatalError() instead of just force unwrapping the optional values makes this intent explicit.
This example is just a thin wrapper around a filter that already exists in Core Image. We can use the same pattern over and over again to create our own filter functions.
Color Overlay
Let’s define a filter that overlays an image with a solid color of our choice. Core Image doesn’t have such a filter by default, but we can compose it from existing filters.
The two building blocks we’re going to use for this are the color generator filter (CIConstantColorGenerator) and the source-over compositing filter (CISourceOverCompositing). Let’s first define a filter to generate a constant color plane:
func generate(color: UIColor) -> Filter {
return { _ in
let parameters = [kCIInputColorKey: CIColor(cgColor: color.cgColor)]
guard let filter = CIFilter(name: "CIConstantColorGenerator",
withInputParameters: parameters)
else { fatalError() }
guard let outputImage = filter.outputImage
else { fatalError() }
return outputImage
}
}
This looks very similar to the blur filter we’ve defined above, with one notable difference: the constant color generator filter doesn’t inspect its input image. Therefore, we don’t need to name the image parameter in the function being returned. Instead, we use an unnamed parameter, _, to emphasize that the image argument to the filter we’re defining is ignored.
Next, we’re going to define the composite filter:
func compositeSourceOver(overlay: CIImage) -> Filter {
return { image in
let parameters = [
kCIInputBackgroundImageKey: image,
kCIInputImageKey: overlay
]
guard let filter = CIFilter(name: "CISourceOverCompositing",
withInputParameters: parameters)
else { fatalError() }
guard let outputImage = filter.outputImage
else { fatalError() }
return outputImage.cropped(to: image.extent)
}
}
Here we crop the output image to the size of the input image. This isn’t strictly necessary, and it depends on how we want the filter to behave. However, this choice works well in the examples we’ll cover.
Finally, we combine these two filters to create our color overlay filter:
func overlay(color: UIColor) -> Filter {
return { image in
let overlay = generate(color: color)(image).cropped(to: image.extent)
return compositeSourceOver(overlay: overlay)(image)
}
}
Once again, we return a function that takes an image parameter as its argument. This function starts by generating an overlay image. To do this, we use our previously defined color generator filter, generate(color:). Calling this function with a color as its argument returns a result of type Filter. Since the Filter type is itself a function from CIImage to CIImage, we can call the result of generate(color:) with image as its argument to compute a new overlay, CIImage.
Constructing the return value of the filter function has the same structure: first we create a filter by calling compositeSourceOver(overlay:). Then we call this filter with the input image.
Composing Filters
Now that we have a blur and a color overlay filter defined, we can put them to use on an actual image in a combined way: first we blur the image, and then we put a red overlay on top. Let’s load an image to work on:
let url = URL(string: "http://via.placeholder.com/500x500")!
let image = CIImage(contentsOf: url)!
Now we can apply both filters to these by chaining them together:
let radius = 5.0
let color = UIColor.red.withAlphaComponent(0.2)
let blurredImage = blur(radius: radius)(image)
let overlaidImage = overlay(color: color)(blurredImage)
Once again, we assemble images by creating a filter, such as blur(radius: radius), and applying the result to an image.
Function Composition
Of course, we could simply combine the two filter calls in the above code in a single expression:
let result = overlay(color: color)(blur(radius: radius)(image))
However, this becomes unreadable very quickly with all these parentheses involved. A nicer way to do this is to build a function that composes two filters into a new filter:
func compose(filter filter1: @escaping Filter,
with filter2: @escaping Filter) -> Filter
{
return { image in filter2(filter1(image)) }
}
The compose(filter:with:) function takes two argument filters and returns a new filter. The resulting composite filter expects an argument image of type CIImage and passes it through both filter1 and filter2, respectively. Here’s an example of how we can use compose(filter:with:) to define our own composite filters:
let blurAndOverlay = compose(filter: blur(radius: radius),
with: overlay(color: color))
let result1 = blurAndOverlay(image)
We can go one step further and introduce a custom operator for filter composition. Granted, defining your own operators all over the place doesn’t necessarily contribute to the readability of your code. However, filter composition is a recurring task in an image processing library. Once you know this operator, it’ll make filter definitions much more readable:
infix operator >>>
func >>>(filter1: @escaping Filter, filter2: @escaping Filter) -> Filter {
return { image in filter2(filter1(image)) }
}
Now we can use the >>> operator in the same way we used compose(filter:with:) before:
let blurAndOverlay2 =
blur(radius: radius) >>> overlay(color: color)
let result2 = blurAndOverlay2(image)
Since the >>> operator is left-associative by default, we can read the filters that are applied to an image from left to right, just like Unix pipes.
The filter composition operation that we’ve defined is an example of function composition. In mathematics, the composition of the two functions f and g, sometimes written f ∘ g, defines a new function mapping an input x to f(g(x)). With the exception of the order, this is precisely what our >>> operator does: it passes an argument image through its two constituent filters.
Theoretical Background: Currying
In this chapter, we’ve repeatedly written code like this:
blur(radius: radius)(image)
First we call a function that returns a function (a Filter in this case), and then we call this resulting function with another argument. We could’ve written the same thing by simply passing two arguments to the blur function and returning the image directly:
let blurredImage = blur(image: image, radius: radius)
Why did we take the seemingly more complicated route and write a function that returns a function, just to call the returned function again?
It turns out there are two equivalent ways to define a function that takes two (or more) arguments. The first style is familiar to most programmers:
func add1(_ x: Int, _ y: Int) -> Int {
return x + y
}
The add1 function takes two integer arguments and returns their sum. In Swift, however, we can define another version of the same function:
func add2(_ x: Int) -> ((Int) -> Int) {
return { y in x + y }
}
The function add2 takes one argument, x, and returns a closure, expecting a second argument, y. This is exactly the same structure we used for our filter functions.
Because the function arrow is right-associative, we can remove the parentheses around the result function type. As a result, the function add3 is exactly the same as add2:
func add3(_ x: Int) -> (Int) -> Int {
return { y in x + y }
}
The difference between the two versions of add lies at the call site:
add1(1, 2) // 3
add2(1)(2) // 3
In the first case, we pass both arguments to add1 at the same time; in the second case, we first pass the first argument, 1, which returns a function, which we then apply to the second argument, 2. Both versions are equivalent: we can define add1 in terms of add2, and vice versa.
The add1 and add2 examples show how we can always transform a function that expects multiple arguments into a series of functions that each expects one argument. This process is referred to as currying, named after the logician Haskell Curry; we say that add2 is the curried version of add1.
So why is currying interesting? As we’ve seen in this book thus far, there are scenarios where you want to pass functions as arguments to other functions. If we have uncurried functions, like add1, we can only apply a function to both its arguments at the same time. On the other hand, for a curried function, like add2, we have a choice: we can apply it to one or two arguments.
The functions for creating filters that we’ve defined in this chapter have all been curried — they all expected an additional image argument. By writing our filters in this style, we were able to compose them easily using the >>> operator. Had we instead worked with uncurried versions of the same functions, it still would’ve been possible to write the same filters. These filters, however, would all have a slightly different type, depending on the arguments they expect. As a result, it’d be much harder to define a single composition operator for the many different types that our filters might have.
Discussion
This example illustrates, once again, how we break complex code into small pieces, which can all be reassembled using function application. The goal of this chapter was not to define a complete API around Core Image, but instead to sketch out how higher-order functions and function composition can be used in a more practical case study.
Why go through all this effort? It’s true that the Core Image API is already mature and provides all the functionality you might need. But in spite of this, we believe there are several advantages to the API designed in this chapter:
Safety — using the API we’ve sketched, it’s almost impossible to create runtime errors arising from undefined keys or failed casts.
Modularity — it’s easy to compose filters using the
>>>operator. Doing so allows you to tease apart complex filters into smaller, simpler, reusable components. Additionally, composed filters have the exact same type as their building blocks, so you can use them interchangeably.Clarity — even if you’ve never used Core Image, you should be able to assemble simple filters using the functions we’ve defined. You don’t need to worry about initializing certain keys, such as
kCIInputImageKeyorkCIInputRadiusKey. From the types alone, you can almost figure out how to use the API, even without further documentation.
Our API presents a series of functions that can be used to define and compose filters. Any filters that you define are safe to use and reuse. Each filter can be tested and understood in isolation. We believe these are compelling reasons to favor the design sketched here over the original Core Image API.
Map, Filter, Reduce
Functions that take functions as arguments are sometimes called higher-order functions. In this chapter, we’ll tour some of the higher-order functions on arrays from the Swift standard library. By doing so, we’ll introduce Swift’s generics and show how to assemble complex computations on arrays.
Optionals
Swift’s optional types can be used to represent values that may be missing or computations that may fail. This chapter describes how to work with optional types effectively and how they fit well within the functional programming paradigm.
Case Study: QuickCheck
In recent years, testing has become much more prevalent in Objective-C. Many popular libraries are now tested automatically with continuous integration tools. The standard framework for writing unit tests is XCTest. Additionally, a lot of third-party frameworks (such as Specta, Kiwi, and FBSnapshotTestCase) are already available, and a number of new frameworks are currently being developed in Swift.
All of these frameworks follow a similar pattern: tests typically consist of some fragment of code, together with an expected result. The code is then executed, and its result is compared to the expected result defined in the test. Different libraries test at different levels — some test individual methods, some test classes, and some perform integration testing (running the entire app). In this chapter, we’ll build a small library for property-based testing of Swift functions. We’ll build this library in an iterative fashion, improving it step by step.
When writing unit tests, the input data is static and defined by the programmer. For example, when unit testing an addition method, we might write a test that verifies that 1 + 1 is equal to 2. If the implementation of addition changes in such a way that this property is broken, the test will fail. More generally, however, we could choose to test that the addition is commutative — in other words, that a + b is equal to b + a. To test this, we could write a test case that verifies that 42 + 7 is equal to 7 + 42.
QuickCheck (Claessen and Hughes 2000) is a Haskell library for random testing. Instead of writing individual unit tests, each of which tests that a function is correct for some particular input, QuickCheck allows you to describe abstract properties of your functions and generate tests to verify these properties. When a property passes, it doesn’t necessarily prove that the property is correct. Rather, QuickCheck aims to find boundary conditions that invalidate the property. In this chapter, we’ll build a (partial) Swift port of QuickCheck.
This is best illustrated with an example. Suppose we want to verify that addition is a commutative operation. To do so, we start by writing a function that checks whether x + y is equal to y + x for the two integers x and y:
func plusIsCommutative(x: Int, y: Int) -> Bool {
return x + y == y + x
}
Checking this statement with QuickCheck is as simple as calling the check function:
check("Plus should be commutative", plusIsCommutative)
// "Plus should be commutative" passed 10 tests.
The Value of Immutability
Swift has several mechanisms for controlling how values may change. In this chapter, we’ll explain how these different mechanisms work, distinguish between value types and reference types, and argue why it’s a good idea to limit the usage of global, mutable state.
Enumerations
Throughout this book, we want to emphasize the important role types play in the design and implementation of Swift applications. In this chapter, we’ll describe Swift’s enumerations, which enable you to craft precise types representing the data your application uses.
Purely Functional Data Structures
In the previous chapter, we saw how to use enumerations to define specific types tailored to the application you’re developing. In this chapter, we’ll define recursive enumerations and show how these can be used to define data structures that are both efficient and persistent.
Case Study: Diagrams
In this chapter, we’ll look at a functional way to describe diagrams and discuss how to draw them with Core Graphics. By wrapping Core Graphics with a functional layer, we get an API that’s simpler and more composable.
Iterators and Sequences
In this chapter, we’ll look at iterators and sequences, which form the machinery underlying Swift’s for loops.
Case Study: Parser Combinators
Case Study: Building a Spreadsheet Application
In this chapter, we’ll expand on the code for parsing arithmetic expressions from the last chapter and build a simple spreadsheet application on top of it. We’ll divide the work into three steps: first we have to write the parser for the expressions we want to support; then we have to write an evaluator for these expressions; and lastly we have to integrate this code into a simple user interface.
Parsing
To build our spreadsheet expression parser, we make use of the parser combinator code we developed in the last chapter. If you haven’t read the previous chapter yet, we recommend you first work through it and then come back here.
Compared to the parser for arithmetic expressions from the last chapter, we’ll introduce one more level of abstraction when parsing spreadsheet expressions. In the last chapter, we wrote our parsers in a way that they immediately return the evaluated result. For example, for multiplication expressions like "2*3" we wrote:
let multiplication = curry({ $0 * ($1 ?? 1) }) <^>
integer <*> (character { $0 == "*" } *> integer).optional
The type of multiplication is Parser<Int>, i.e. executing this parser on the input string "2*3" will return the integer value 6.
Immediately evaluating the result only works as soon as the expressions we parse don’t depend on any data outside of the expression itself. However, in our spreadsheet we want to allow expressions like A3 to reference another cell’s value or function calls like SUM(A1:A3).
To support such features, the parser task is to turn the input string into an intermediate representation of the expression, also referred to as an abstract syntax tree, which describes what’s in the expression. In the next step, we can take this structured data and actually evaluate it.
Functors, Applicative Functors, and Monads
In this chapter, we’ll explain some terminology and common patterns used in functional programming, including functors, applicative functors, and monads. Understanding these common patterns will help you design your own data types and choose the correct functions to provide in your APIs.
Functors
Thus far, we’ve seen a couple of methods named map, with the following types:
extension Array {
func map<R>(transform: (Element) -> R) -> [R]
}
extension Optional {
func map<R>(transform: (Wrapped) -> R) -> R?
}
extension Parser {
func map<T>(_ transform: @escaping (Result) -> T) -> Parser<T>
}
Why have three such different functions with the same name? To answer that question, let’s investigate how these functions are related. To begin with, it helps to expand some of the shorthand notation Swift uses. Optional types, such as Int?, can also be written out explicitly as Optional<Int> in the same way we can write Array<T> rather than [T]. If we now state the types of the map function on arrays and optionals, the similarity becomes more apparent:
extension Array {
func map<R>(transform: (Element) -> R) -> Array<R>
}
extension Optional {
func map<R>(transform: (Wrapped) -> R) -> Optional<R>
}
extension Parser {
func map<T>(_ transform: @escaping (Result) -> T) -> Parser<T>
}
Both Optional and Array are type constructors that expect a generic type argument. For instance, Array<T> and Optional<Int> are valid types, but Array by itself is not. Both of these map functions take two arguments: the structure being mapped, and a function transform of type (T) -> U. The map functions use a function argument to transform all the values of type T to values of type U in the argument array or optional. Type constructors — such as optionals or arrays — that support a map operation are sometimes referred to as functors.
In fact, there are many other types we’ve defined that are indeed functors. For example, we can implement a map function on the Result type from Chapter 8:
extension Result {
func map<U>(f: (T) -> U) -> Result<U> {
switch self {
case let .success(value): return .success(f(value))
case let .error(error): return .error(error)
}
}
}
Similarly, the types we’ve seen for binary search trees, tries, and parser combinators are all functors. Functors are sometimes described as ‘containers’ storing values of some type. The map functions transform the stored values stored in a container. This can be a useful intuition, but it can be too restrictive. Remember the Region type we saw in Chapter 2?
struct Position {
var x: Double
var y: Double
}
typealias Region = (Position) -> Bool
Using this definition of regions, we can only generate black and white bitmaps. We can generalize this to abstract over the kind of information we associate with every position:
struct Region<T> {
let value: (Position) -> T
}
Using this definition, we can associate booleans, RGB values, or any other information with every position. We can also define a map function on these generic regions. Essentially, this definition boils down to function composition:
extension Region {
func map<U>(transform: @escaping (T) -> U) -> Region<U> {
return Region<U> { pos in transform(self.value(pos)) }
}
}
Such regions are a good example of a functor that doesn’t fit well with the intuition of functors being containers. Here, we’ve represented regions as functions, which seem very different from containers.
Almost every generic enumeration you can define in Swift will be a functor. Providing a map function gives fellow developers a powerful yet familiar function for working with such enumerations.
Applicative Functors
Many functors also support other operations aside from map. For example, the parsers from Chapter 12 weren’t only functors, but they also defined the following operation:
func <*><A, B>(lhs: Parser<(A) -> B>, rhs: Parser<A>)
-> Parser<B> {
The <*> operator sequences two parsers: the first parser returns a function, and the second parser returns an argument for this function. The choice for this operator is no coincidence. Any type constructor for which we can define appropriate pure and <*> operations is called an applicative functor. To be more precise, a functor F is applicative when it supports the following operations:
func pure<A>(_ value: A) -> F<A>
func <*><A, B>(f: F<A -> B>, x: F<A>) -> F<B>
We didn’t define pure for Parser, but it’s very easy to do so yourself. Applicative functors have been lurking in the background throughout this book. For example, the Region struct defined above is also an applicative functor:
precedencegroup Apply { associativity: left }
infix operator <*>: Apply
func pure<A>(_ value: A) -> Region<A> {
return Region { pos in value }
}
func <*><A, B>(regionF: Region<(A) -> B>, regionX: Region<A>) -> Region<B> {
return Region { pos in regionF.value(pos)(regionX.value(pos)) }
}
Now the pure function always returns a constant value for every region. The <*> operator distributes the position to both its region arguments, which yields a function of type A -> B and a value of type A. It then combines these in the obvious manner, by applying the resulting function to the argument.
Many of the functions defined on regions can be described succinctly using these two basic building blocks. Here are a few example functions — inspired by Chapter 2 — written in applicative style:
func everywhere() -> Region<Bool> {
return pure(true)
}
func invert(region: Region<Bool>) -> Region<Bool> {
return pure(!) <*> region
}
func intersection(region1: Region<Bool>, region2: Region<Bool>)
-> Region<Bool>
{
let and: (Bool, Bool) -> Bool = { $0 && $1 }
return pure(curry(and)) <*> region1 <*> region2
}
This shows how the applicative instance for the Region type can be used to define pointwise operations on regions.
Applicative functors aren’t limited to regions and parsers. Swift’s built-in optional type is another example of an applicative functor. The corresponding definitions are fairly straightforward:
func pure<A>(_ value: A) -> A? {
return value
}
func <*><A, B>(optionalTransform: ((A) -> B)?, optionalValue: A?) -> B? {
guard let transform = optionalTransform,
let value = optionalValue else { return nil }
return transform(value)
}
The pure function wraps a value into an optional. This is usually handled implicitly by the Swift compiler, so it’s not very useful to define ourselves. The <*> operator is more interesting: given a (possibly nil) function and a (possibly nil) argument, it returns the result of applying the function to the argument when both exist. If either argument is nil, the whole function returns nil. We can give similar definitions for pure and <*> for the Result type from Chapter 8.
By themselves, these definitions may not be very interesting, so let’s revisit some of our previous examples. You may want to recall the addOptionals function, which tried to add two possibly nil integers:
func addOptionals(optionalX: Int?, optionalY: Int?) -> Int? {
guard let x = optionalX, y = optionalY else { return nil }
return x + y
}
Using the definitions above, we can give a short alternative definition of addOptionals using a single return statement:
func addOptionals(optionalX: Int?, optionalY: Int?) -> Int? {
return pure(curry(+)) <*> optionalX <*> optionalY
}
Once you understand the control flow that operators like <*> encapsulate, it becomes much easier to assemble complex computations in this fashion.
There’s one other example from the optionals chapter that we’d like to revisit:
func populationOfCapital(country: String) -> Int? {
guard let capital = capitals[country], population = cities[capital]
else { return nil }
return population * 1000
}
Here we consulted one dictionary, capitals, to retrieve the capital city of a given country. We then consulted another dictionary, cities, to determine each city’s population. Despite the obvious similarity to the previous addOptionals example, this function cannot be written in applicative style. Here’s what happens when we try to do so:
func populationOfCapital(country: String) -> Int? {
return { pop in pop * 1000 } <*> capitals[country] <*> cities[...]
}
The problem is that the result of the first lookup, which was bound to the capital variable in the original version, is needed in the second lookup. Using only the applicative operations, we quickly get stuck: there’s no way for the result of one applicative computation (capitals[country]) to influence another (the lookup in the cities dictionary). To deal with this, we need yet another interface.
The M-Word
In Chapter 5, we gave the following alternative definition of populationOfCapital:
func populationOfCapital3(country: String) -> Int? {
return capitals[country].flatMap { capital in
return cities[capital]
}.flatMap { population in
return population * 1000
}
}
Here we used the built-in flatMap function to combine optional computations. How is this different from the applicative interface? The types are subtly different. In the applicative <*> operation, both arguments are optionals. In the flatMap function, on the other hand, the second argument is a function that returns an optional value. Consequently, we can pass the result of the first dictionary lookup on to the second.
The flatMap function is impossible to define in terms of the applicative functions. In fact, the flatMap function is one of the two functions supported by monads. More generally, a type constructor F is a monad if it defines the following two functions:
func pure<A>(_ value: A) -> F<A>
func flatMap<A, B>(x: F<A>)(_ f: (A) -> F<B>) -> F<B>
The flatMap function is sometimes defined as an operator, >>=. This operator is pronounced “bind,” as it binds the result of the first argument to the parameter of its second argument.
In addition to Swift’s optional type, the Result enumeration defined in Chapter 8 is also a monad. This insight makes it possible to chain together computations that may return an Error. For example, we could define a function that copies the contents of one file to another as follows:
func copyFile(sourcePath: String, targetPath: String, encoding: Encoding)
-> Result<()>
{
return readFile(sourcePath, encoding).flatMap { contents in
writeFile(contents, targetPath, encoding)
}
}
If the call to either readFile or writeFile fails, the Error will be logged in the result. This may not be quite as nice as Swift’s optional binding mechanism, but it’s still pretty close.
There are many other applications of monads aside from handling errors. For example, arrays are also a monad. In the standard library, flatMap is already defined, but you could implement it like this:
func pure<A>(_ value: A) -> [A] {
return [value]
}
extension Array {
func flatMap<B>(_ f: (Element) -> [B]) -> [B] {
return map(f).reduce([]) { result, xs in result + xs }
}
}
What have we gained from these definitions? The monad structure of arrays provides a convenient way to define various combinatorial functions or solve search problems. For example, suppose we need to compute the cartesian product of two arrays, xs and ys. The cartesian product consists of a new array of tuples, where the first component of the tuple is drawn from xs, and the second component is drawn from ys. Using a for loop directly, we might write this:
func cartesianProduct1<A, B>(xs: [A], ys: [B]) -> [(A, B)] {
var result: [(A, B)] = []
for x in xs {
for y in ys {
result += [(x, y)]
}
}
return result
}
We can now rewrite cartesianProduct to use flatMap instead of for loops:
func cartesianProduct2<A, B>(xs: [A], ys: [B]) -> [(A, B)] {
return xs.flatMap { x in ys.flatMap { y in [(x, y)] } }
}
The flatMap function allows us to take an element x from the first array, xs; next, we take an element y from ys. For each pair of x and y, we return the array [(x, y)]. The flatMap function handles combining all these arrays into one large result.
While this example may seem a bit contrived, the flatMap function on arrays has many important applications. Languages like Haskell and Python support special syntactic sugar for defining lists, which are called list comprehensions. These list comprehensions allow you to draw elements from existing lists and check that these elements satisfy certain properties. They can all be de-sugared into a combination of maps, filters, and flatMap. List comprehensions are very similar to optional binding in Swift, except they work on lists instead of optionals.
Discussion
Why care about these things? Does it really matter if you know that some type is an applicative functor or a monad? We think it does.
Consider the parser combinators from Chapter 12. Defining the correct way to sequence two parsers isn’t easy: it requires a bit of insight into how parsers work. Yet it’s an absolutely essential piece of our library, without which we couldn’t even write the simplest parsers. If you have the insight that our parsers form an applicative functor, you may realize that the existing <*> provides you with exactly the right notion of sequencing two parsers, one after the other. Knowing what abstract operations your types support can help you find such complex definitions.
Abstract notions, like functors, provide important vocabulary. If you ever encounter a function named map, you can probably make a pretty good guess as to what it does. Without a precise terminology for common structures like functors, you would have to rediscover each new map function from scratch.
These structures give guidance when designing your own API. If you define a generic enumeration or struct, chances are that it supports a map operation. Is this something you want to expose to your users? Is your data structure also an applicative functor? Is it a monad? What do the operations do? Once you familiarize yourself with these abstract structures, you see them pop up again and again.
Although it’s more difficult in Swift than in Haskell, you can define generic functions that work on any applicative functor. Functions such as the <^> operator on parsers can be defined exclusively in terms of the applicative pure and <*> functions. As a result, we may want to redefine them for other applicative functors aside from parsers. In this way, we recognize common patterns in how we program using these abstract structures; these patterns may themselves be useful in a wide variety of settings.
The historical development of monads in the context of functional programming is interesting. Initially, monads were developed in a branch of mathematics known as category theory. The discovery of their relevance to computer science is generally attributed to Moggi (1991), a fact that was later popularized by Wadler (1992a; 1992b). Since then, they’ve been used by functional languages such as Haskell to contain side effects and I/O (Peyton Jones 2001). Applicative functors were first described by McBride and Paterson (2008), although there were many examples already known. A complete overview of the relation between many of the abstract concepts described in this chapter can be found in the Typeclassopedia (Yorgey 2009).
Conclusion
So what is functional programming? Many people (mistakenly) believe functional programming is only about programming with higher-order functions, such as map and filter. There is much more to it than that.
In the Introduction, we mentioned three qualities that we believe characterize well-designed functional programs in Swift: modularity, a careful treatment of mutable state, and types. In each of the chapters we have seen, these three concepts pop up again and again.
Higher-order functions can certainly help define some abstractions, such as the Filter type in Chapter 3 or the regions in Chapter 2, but they are a means, not an end. The functional wrapper around the Core Image library we defined provides a type-safe and modular way to assemble complex image filters. Generators and sequences (Chapter 11) help us abstract iteration.
Swift’s advanced type system can help catch many errors before your code is even run. Optional types (Chapter 5) mark possible nil values as suspicious; generics not only facilitate code reuse, but also allow you to enforce certain safety properties (Chapter 4); and enumerations and structs provide the building blocks to model the data in your domain accurately (Chapters 8 and 9).
Referentially transparent functions are easier to reason about and test. Our QuickCheck library (Chapter 6) shows how we can use higher-order functions to generate random unit tests for referentially transparent functions. Swift’s careful treatment of value types (Chapter 7) allows you to share data freely within your application without having to worry about it changing unintentionally or unexpectedly.
We can use all these ideas in concert to build powerful domain-specific languages. Our libraries for diagrams (Chapter 10) and parser combinators (Chapter 12) both define a small set of functions, providing the modular building blocks that can be used to assemble solutions to large and difficult problems. Our final case study shows how these domain-specific languages can be used in a complete application (Chapter 13).
Finally, many of the types we have seen share similar functions. In Chapter 14, we show how to group them and how they relate to each other.
Further Reading
One way to further hone your functional programming skills is by learning Haskell. There are many other functional languages, such as F#, OCaml, Standard ML, Scala, or Racket, each of which would make a fine choice of language to complement Swift. Haskell, however, is the most likely to challenge your preconceptions about programming. Learning to program well in Haskell will change the way you work in Swift.
There are a lot of Haskell books and courses available these days. Graham Hutton’s Programming in Haskell (2007) is a great starting point to familiarize yourself with the language basics. Learn You a Haskell for Great Good! is free to read online and covers some more advanced topics. Real World Haskell describes several larger case studies and a lot of the technology missing from many other books, including support for profiling, debugging, and automated testing. Richard Bird is famous for his “functional pearls” — elegant, instructive examples of functional programming, many of which can be found in his book, Pearls of Functional Algorithm Design (2010), or online. Finally, The Fun of Programming is a collection of domain-specific languages embedded in Haskell, covering domains ranging from financial contracts to hardware design (Gibbons and de Moor 2003).
If you want to learn more about programming language design in general, Benjamin Pierce’s Types and Programming Languages (2002) is an obvious choice. Bob Harper’s Practical Foundations for Programming Languages (2012) is more recent and more rigorous, but unless you have a solid background in computer science or mathematics, you may find it hard going.
Don’t feel obliged to make use of all of these resources; many of them may not be of interest to you. But you should be aware that there is a huge amount of work on programming language design, functional programming, and mathematics that has directly influenced the design of Swift.
If you’re interested in further developing your Swift skills – not only the functional parts of it – we’ve written an entire book about advanced swift topics, covering topics low-level programming to high-level abstractions.
Closure
This is an exciting time for Swift. The language is still very much in its infancy. Compared to Objective-C, there are many new features — borrowed from existing functional programming languages — that have the potential to dramatically change the way we write software for iOS and OS X.
At the same time, it is unclear how the Swift community will develop. Will people embrace these features? Or will they write the same code in Swift as they do in Objective-C, but without the semicolons? Time will tell. By writing this book, we hope to have introduced you to some concepts from functional programming. It is up to you to put these ideas in practice as we continue to shape the future of Swift.